Poker Hands Heads Up Probability
In this article we define and publish the exact pre-flop probabilities for each possible combination of two hands in Textas Hold’em poker. An online tool at tools.timodenk.com/poker-odds-pre-flop makes the data visually accessible.
Table of Contents
Introduction
A deck of French playing cards, as it is used in Texas Hold’em, contains 52 different cards; in a heads-up game two players are playing against each other. Both of them get two private cards dealt pre-flop face down. There are $binom{52}{2}=1326$ different possible pairs of cards that players can get. In this work we determine the odds of each starting hand to win against any other starting hand. There is no equation or easy way of calculating the winning probability of a given hand, since it would be required to contain all the rules and mechanics of the game.
When comparing two starting hands, the head-to-head probability describes the likelihood of one hand beating the other after all of the cards have come out. Head-to-head probabilities vary slightly for each particular distinct starting hand matchup, but the approximate average probabilities are summarized in the following table. Texas Holdem Heads-Up Preflop Odds. This table was created by enumerating through every possible board and opponent hole card combination for each of the 169 texas holdem preflop starting hands. See full list on wizardofodds.com.
Statistical approaches can determine the winning odds of one starting hand against another very quickly. This gives results that are statistically accurate but not guaranteed to be exact. However, for mathematical analysis of certain properties of pre-flop situations, the precise numbers are a requirement.
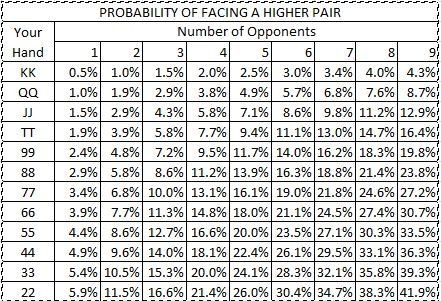
As I mentioned in tip #1, the starting hand values go way up in heads up poker. The same goes for showdown hands. The average winning hand in heads up poker will be much worse than the average winning hand at a 9-handed game, so adjust accordingly.
Win Function
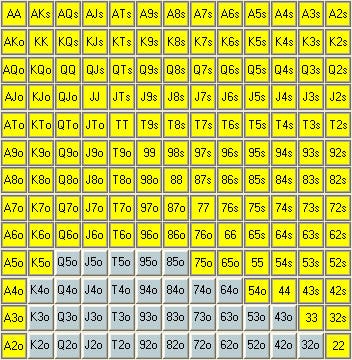
Hold’em cards can have 13 different ranks and four different suits
$$begin{align}
mathcal{R}=&left{text{Ace}, text{2}, text{3}, text{4}, text{5}, text{6}, text{7}, text{8}, text{9}, text{10}, text{Jack}, text{Queen}, text{King}right},
mathcal{S}=&left{text{Club}, text{Heart}, text{Spade}, text{Diamond}right},.end{align}$$A card is an ordered pair of rank and suit; the set of all cards that exist in a the card deck is denoted as
$$begin{align}mathcal{C}=mathcal{R}timesmathcal{S},end{align}$$ with $leftlvertmathcal{C}rightrvert=52$. The set of possible starting hands, every possible combination of two distinct cards, is defined by
$$begin{align}mathcal{H}=left{left{c_1inmathcal{C},c_2inmathcal{C}right}mid c_1neq c_2right}end{align}$$ and has a cardinality of $lvertmathcal{H}rvert=binom{52}{2}=1326$. The set is containing unordered pairs because the two private cards are not ordered either.
Calculating the Cartesian product of the set of possible hands with itself gives a new set of ordered pairs, that is $mathcal{M}=mathcal{H}timesmathcal{H}$, with $leftlvertmathcal{M}rightrvert=1,758,276$. This set contains all combinations of two starting hands as ordered pairs. The order matters, because we define the meaning of each of the pairs as a pre-flop situation where the first starting hand plays against the second.
In this work we search for the winning odds function
$$begin{align}
o:mathcal{M}rightarrowleft{xinmathbb{Q}mid0le xle1right},
end{align}$$ that outputs for any pre-flop situation $left(h_1,h_2right)$, the odds of starting hand $h_1$ to win against $h_2$. Since every card exists only once in a deck, two players cannot play against each other if $h_1cap h_2neemptyset$. For these cases $o$ is undefined.
Post-flop, five community cards are dealt. Three on the flop, followed by the turn card, and finally the river card. $binom{52}{5}=2598960$ different combinations are possible. We define $mathcal{P}$ as the set of all possible community cards, where each $pinmathcal{P}$ is itself a set of five different cards. The community cards $p$ determine which player wins, that is the one whose starting hand builds the best showdown hand. If both showdown hands are of equal rank at showdown, the pot is split. Given a pre-flop situation $m=(h_1,h_2)$ where the starting hand $h_1$ plays against $h_2$, only a subset of $mathcal{P}$, namely $$begin{align}mathcal{P}_{(h_1,h_2)}=left{pinmathcal{P}mid pcap h_1=pcap h_2=emptysetright}end{align}$$ can be dealt, as some cards are already taken from the deck.
Furthermore a win function
$$begin{align}w:{(minmathcal{M},pinmathcal{P}_m)}rightarrow{0,1}end{align}$$is required, that assesses a situation at showdown and returns $1$, if the first starting hand in $m$ wins against the second hand, given the public cards $p$. In case of loss or split it returns $0$. $w$ is defined by the rules of poker. With these definitions at hand we can define the odds of a hand to win against another hand as
$$begin{align}o(m)=frac{displaystylesum_{pinmathcal{P}_m}w(m,p)}{lvert mathcal{P}_mrvert},.end{align}$$In words, $o$ is dividing the number of possible community cards where $h_1$ wins against $h_2$ by the number of community cards that can be dealt altogether.
Data and Results
With the odds function $o$ at hand, we can define the winning odds matrix $mathbf{M}inmathbb{Q}^{lvertmathcal{H}rverttimeslvertmathcal{H}rvert}$ as
$$M_{i,j}=o(mathcal{H}_i,mathcal{H}_j),.$$ The matrix contains the winning odds for every heads-up pre-flop situation and is undefined at places, where $mathcal{H}_i$ and $mathcal{H}_j$ cannot play against each other (because of shared cards). From its row vectors, i.e. $mathbf{M}_{i,:}$, we can compute the average odds of a hand $mathcal{H}_i$ to win against a random hand, by taking the average of all entries with values. The probabilities for a split between two hands are given by $1-M_{i,j}-M_{j,i}$.
We release $mathbf{M}$ in two ways.
- As an online tool with user interface at tools.timodenk.com where the user can pick their pre-flop situation and get the exact odds, i.e. $o(m)$ and $o(m)lvertmathcal{P}_mrvert$.
- As a serialized Java object holding the $o(m)lvertmathcal{P}_mrvert$ values for every $m$. The object can be imported into a Java program and processed from there.
We have already conducted some experiments related to the non-transitivity of the win function. For example, we found the three hands
$$begin{align}
h_1=&left{left(text{Ace},text{Club}right),left(text{2},text{Club}right)right}
h_2=&left{left(text{10},text{Spade}right),left(text{9},text{Spade}right)right}
h_3=&left{left(text{2},text{Heart}right),left(text{2},text{Diamond}right)right},
end{align}$$to satisfy$$begin{align}
oleft(h_1,h_2right)approx&0.54gt0.5
oleft(h_2,h_3right)approx&0.53gt0.5
oleft(h_3,h_1right)approx&0.61gt0.5,.
end{align}$$Expressed in words, this means for a hand $h_1$, which statistically beats $h_2$, which in turn beats a third hand $h_3$, it cannot be concluded that $h_1$ beats $h_3$ as well. The win function is not transitive.
Heads-up Match-ups In Hold’em Pokerology.com
The most uneven pre-flop situation exists, if the hands$$begin{align}
h_1=&left{left(text{King},text{Club}right),left(text{King},text{Diamond}right)right}
h_2=&left{left(text{King},text{Heart}right),left(text{2},text{Club}right)right}
end{align}$$play against each other (or suit permutations). The pair of kings has a $94.16%$ chance of winning. The pot is chopped in $1.53%$ of all possible outcomes.
Surprisingly, Aces do not appear in this constellation. The reason is that the hand A2 could hit a straight with just three cards (3, 4, 5). On the other hand, K2 needs four cards (A, 3, 4, 5 or 3, 4, 5, 6) in order to build a straight that uses the 2. Also noteworthy is the fact, that the King of Clubs of $h_1$ blocks flushes, which $h_2$ could have otherwise gotten using the Deuce of Clubs.
The lowest winning probability and highest probability for a split pot exists if $$begin{align}
h_1=&left{left(text{3},text{Club}right),left(text{2},text{Diamond}right)right}
h_2=&left{left(text{3},text{Diamond}right),left(text{2},text{Club}right)right}
end{align}$$battle each other. Both hands have an equal chance of winning, namely $0.71%$. Consequently, a split occurs with a likelihood of $98.57%$.
Interestingly, the get-together of 43 vs. 43 (same suits as above) comes with a higher winning probability ($0.73%$). That’s (at least partly) because there are a few more flushes, for which one of the hands does not only play the board.
The lowest split probability of just $0.19%$ is there, if the following hands play:$$begin{align}
h_1=&left{left(text{9},text{Club}right),left(text{8},text{Diamond}right)right}
h_2=&left{left(text{Ace},text{Spade}right),left(text{Ace},text{Heart}right)right},.
end{align}$$In which cases would the pot be chopped? For instance if a straight flush of Clubs from 2 to 6 occurs.
Still unsolved is the search for the longest non-transitive chain of mutually disjoint pre-flop hands, such that $$o(h_1, h_2)>0.5land o(h_2,h_3)>0.5landdotsland o(h_n,h_1)>0.5,.$$
Special thanks goes to Dominik Müller for fruitful discussions and many algorithm optimization ideas.
If you're new to the heads up game, you can really get crushed by rushing in blindly. Proper heads up strategy is vastly different than normal No Limit Hold'em Strategy, and you need to make the correct adjustments in order to beat your opponents and make money. I recommend following the 10 tips below to help you get started and learn the basics, then read the rest of our heads up poker strategy to fine tune your game. Good luck.
Tip #1 - Open it Up
The first tip you need is to open up your starting hand ranges. Since you only have two players at the table, the average starting hand that sees the flop is going to be much worse than at a normal 9-handed table. Because of this you should open up your starting hand range.
You can't afford to wait for premium hands while playing heads up because you're in the blinds every hand. I recommend playing the majority of your hands as the big blind, and playing damn near every single hand when you're the dealer. Learn more differences between heads up and 9 handed poker.
Tip #2 - Play Your Position
Position becomes a huge factor in heads up poker, because you are either in the best position or in the worst position every hand: there is no in between. Like I mentioned before, I recommend playing every single hand when you're in dealer position. When you're the dealer, you'll post the small blind, act first preflop, and act last on the flop and beyond. When you're the small blind, you'll post the big blind, act last preflop, and act first on the flop and beyond.
Because of this, you want to be really aggressive preflop as the dealer, and raise with a wide range of hands (think any pocket pair, any suited connector, and two big cards, etc). Also, you should be more conservative as the big blind, and respect raises from the dealer.
Tip #3 - Remember Hand Values
As I mentioned in tip #1, the starting hand values go way up in heads up poker. The same goes for showdown hands. The average winning hand in heads up poker will be much worse than the average winning hand at a 9-handed game, so adjust accordingly. Even hands like middle pair or second worst pair are still decent hands and will probably win an uncontested pot, so bet them out.
Tip #4 - Semi-Bluff When Possible
A great way to pick up a bunch of pots in heads up poker is by firing out smallish bets into un raised pots. When I'm playing heads up I like to bet a ton of flops as long as I get any piece; even a straight draw or bottom pair is worth taking a shot on the flop. If my opponent calls I'll slow down, but most passive opponents will toss basically any hand but top pair or maybe second pair to a bet.
Tip #5 - Spot Bluff Attempts
This is basically the opposite of the above tip. If you're playing an aggressive opponent, you'll have to make a stand to prevent constant semi-bluffs and preflop raises. I like to re-raise on occasion preflop, and to call the majority of the flop bets to see if my opponent will bet again on the turn and river. Even if you only have middle pair you should look him/her up to keep them honest, or he/she will continue to pummel you in every pot.
Tip #6 - Make Value Bets
This relates to tip #3 because with lower winning hands you'll have to extract value from hands you normally wouldn't. For example, when you have middle pair on the river you should bet because it is likely you're ahead and will get called by third pair or worse. Also, when you have an extremely strong hand I like to make small bets on the flop, turn, and a larger bet on the river to get maximum value out of my opponent by reeling them in.
Tip #7 - Adjust to your Opponent
Throughout the course of a heads up battle, you'll gain reads on your opponent, and he/she will gain reads on your play as well. As you pick up common plays and tendencies of your opponent, you need to make adjustments to counter their most used moves. For example, if you notice that your opponent is always checking the flop and betting the turn when he/she flops top pair, make sure to fold more on the turn if that same situation comes up.
Tip #8 - Switch up your Game
This is just the opposite of the last tip. As you're picking up reads on your opponent, he/she will be doing the same. Because of this you need to switch up your play to keep them guessing, especially if you are in a long heads up battle that spans over an hour. To keep your opponents on their toes, make sure to alternate between betting flops and checking them when you hit, and throw in an occasional strange play like a big bluff or a check-raise. Learn more about switching up your game.
Tip #9 - Be a Finisher
This is an important tip for heads up players. When you battle your opponent down to a small stack, you have to finish him/her off and not let him/her back into the match. To do this, you can't give them any easy double ups or get lazy and call off big bets. The easiest way to let a crippled opponent back into a match is to call preflop all-ins with a poor hand just to try to knock them out. Continue to play your normal game, and you'll finish them off quickly.
Tip #10 - Stick to Your Bankroll
See All Results For This Question
One common mistake that new players make is playing heads up cash tables with their whole bankroll. This is a big mistake, and will almost surely leave you broke. I recommend never playing with more than 1/10th of your entire bankroll if you're a casual player, or more than 1/50th of your stack if you're a professional or serious player.