Casino House Edge Chart
On This Page
Introduction
- So if it says “0.50”, then the player will have an advantage starting at a true 1, a.5% advantage at a true 2, and a 1% advantage at a true 3. Conversely, the casino would have a 1% advantage at a true -1. Below is a chart that shows how each rule affects the house edge.
- Video poker machines look like slot machines, but they offer a better house edge—if you play the hands optimally. Depending on the pay table, the house edge for video poker can be as low as 0.5% or as high as 5% or 6%. And those are the basics of the house edge as it pertains to casino games.
- Blackjack is traditionally the highest payout casino game and the house edge is minimal. Online blackjack usually uses one or two decks, compared to eight in a land-based casino. This is important.
Let it Ride Odds. The payouts and odds for Let It Ride are used to calculate the normal house edge of 3.51%.Normally, the game is played with a single 52-card deck, so the odds are static; they never change, although the Let It Ride payout tables may change depending on where you play. House edge means the percentage of the player's bet the casino wins on average. This is worth figuring out since the size of house edge has everything to do with how likely you're to win. Educated players always find the games with the least house edge possible and therefore win the most - or at least lose the least.
Casino Hold 'Em is a poker variation, similar to Texas Hold 'Em, that is played in Egypt, Russia, South Africa, Holland, Latvia, Estonia, Ireland, Morocco, Malta, Ukraine, Panama, and Romania. It is also available to play online at casinos using Net Gaming, Real Time Gaming, Playtech, Gamesys, and Galewind Software.
The game also goes by the name Casino Hold 'Em Open. Under this name, the rules are the same except the player hole cards are dealt face up. In normal Casino Hold 'Em they are dealt face down.
Rules
The rules are as follows.
- Play begins with each player making an Ante wager. There is also an optional Progressive Jackpot side bet.
- The dealer gives the player and himself two hole cards and three community cards face up on the table.
- Each player must decide to either fold or call. If the player folds, then he gives up his cards and his Ante bet. If the player calls, then the Call bet must be equal to two times the Ante bet.
- The dealer will then deal two more community cards, for a total of five. The dealer will then turn over his own two cards.
- Both hands shall be scored according the highest poker value of the two hole cards and five community cards.
- The dealer must have a pair of fours or better to qualify. If the dealer does not qualify then the Ante will pay according to the Ante pay table below and the Call bet will push.
- If the dealer qualifies and beats the player, then the player will lose both the Ante and Call.
- If the dealer qualifies and the player beats the dealer then the Ante will pay according to the Ante pay table below and the Call bet will pay 1 to 1.
- If the dealer qualifies and the player ties the dealer then both Ante and Call bets will push.
- The Progressive Jackpot side bet pays based on the player's final seven card hand only, even if the player folded or loses to the dealer. More on this bet at the bottom of the page.
Ante Pay Table
| Hand | Table 1 | Table 2 | Table 3 | Table 4 |
|---|---|---|---|---|
| Royal flush | 20 | 25 | 100 | 100 |
| Straight flush | 20 | 25 | 20 | 49 |
| 4 of a kind | 10 | 12 | 10 | 17 |
| Full house | 3 | 3 | 3 | 3 |
| Flush | 2 | 2 | 2 | 2 |
| All other | 1 | 1 | 1 | 1 |
Caribbean Hold 'Em Warning
Be warned that Realtime Gaming has an imitation of this game called Caribbean Hold 'Em. However, they pay 1 to 1 on the Ante if the dealer doesn't qualify, as opposed to the full Ante Bonus pay table. Nowhere is this rule change disclosed in their game rules, I might add.
Analysis
The following table shows the number of combination, probability, and contribution to the return of all possible outcomes under ante pay table 3, which I'm told is the most frequently used. The lower right cell shows a house edge of 2.16%.
Return Table — Pay Table 3Expand
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Player wins with royal flush | 102 | 736259040 | 0.000026 | 0.002700 |
| Player has royal flush, dealer doesn't qualify | 100 | 119892960 | 0.000004 | 0.000431 |
| Player wins with straight flush | 22 | 6001122284 | 0.000216 | 0.004747 |
| Player has straight flush, dealer doesn't qualify | 20 | 1089672828 | 0.000039 | 0.000784 |
| Player wins with four of a kind | 12 | 41419896552 | 0.001489 | 0.01787 |
| Player has four of a kind, dealer doesn't qualify | 10 | 909499320 | 0.000033 | 0.000327 |
| Player wins with full house | 5 | 589505037660 | 0.021195 | 0.105973 |
| Player wins with flush | 4 | 505131419580 | 0.018161 | 0.072645 |
| Player wins with straight or less | 3 | 6426670016572 | 0.23106 | 0.693181 |
| Player has full house, dealer doesn't qualify | 3 | 24601676832 | 0.000885 | 0.002654 |
| Player has flush, dealer doesn't qualify | 2 | 168883536432 | 0.006072 | 0.012144 |
| Player has straight or less, dealer doesn't qualify | 1 | 5521376219148 | 0.198512 | 0.198512 |
| Tie | 0 | 678596916580 | 0.024398 | 0 |
| Player folds | -1 | 5009067102600 | 0.180093 | -0.180093 |
| Player loses | -3 | 8839701755612 | 0.317817 | -0.953451 |
| Total | 27813810024000 | 1 | -0.021576 |
The following return table is four pay table 4. The lower right cell shows a house edge of 0.35%. This pay table can be found at Internet casinos using Gamesys N.V. software titled 'Casino Hold 'Em with Zero House Edge.' As you can see, the 'Zero House Edge' part is a misnomer. The player must pay a 10% commission on any net gambling win per session. A 'session' ends after a period of one hour with no bet or 24 hours, whichever happens first.
The owner of Casino Hold 'Em wishes for me to state that Gamesys N.V. is using his game without permission.
Return Table — Pay Table 4Expand
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Player wins with royal flush | 102 | 736,259,040 | 0.000026 | 0.002700 |
| Player has royal flush, dealer doesn't qualify | 100 | 119,892,960 | 0.000004 | 0.000431 |
| Player wins with straight flush | 51 | 6,031,161,932 | 0.000217 | 0.011059 |
| Player has straight flush, dealer doesn't qualify | 49 | 1,096,758,936 | 0.000039 | 0.001932 |
| Player wins with four of a kind | 19 | 41,421,337,056 | 0.001489 | 0.028295 |
| Player has four of a kind, dealer doesn't qualify | 17 | 909,634,104 | 0.000033 | 0.000556 |
| Player wins with full house | 5 | 589,638,417,816 | 0.021199 | 0.105997 |
| Player wins with flush | 4 | 505,727,272,920 | 0.018183 | 0.072730 |
| Player wins with straight or less | 3 | 6,429,871,396,516 | 0.231175 | 0.693526 |
| Player has full house, dealer doesn't qualify | 3 | 24,601,738,176 | 0.000885 | 0.002654 |
| Player has flush, dealer doesn't qualify | 2 | 169,051,416,912 | 0.006078 | 0.012156 |
| Player has straight or less, dealer doesn't qualify | 1 | 5,526,154,486,512 | 0.198684 | 0.198684 |
| Tie | 0 | 679,763,871,140 | 0.024440 | 0.000000 |
| Player folds | -1 | 4,984,375,678,920 | 0.179205 | -0.179205 |
| Player loses | -3 | 8,854,310,701,060 | 0.318342 | -0.955027 |
| Total | 27,813,810,024,000 | 1.000000 | -0.003511 |
I would like to thank Stephen How of Discount Gambling for supplying the combinations in pay table 4.
The only pay tables fully analyzed are 3 and 4, because it takes my computer about a month to cycle through all possible combinations. However, assuming the player was following optimal strategy under pay table 3 but playing under pay table 1 or 2, the house edge under pay table 1 would be 2.40%, and under pay table 2 would be 1.96%. The actual house edge under pay tables 1 and 2 would be slightly less or equal to these figures.
Strategy
Unfortunately, there is no easy way to quantify optimal strategy for this game. I can say that the optimal strategy player will raise 82% of the time. So only in the worst 18% of hands should the player fold. In general these are when the player has two singletons in the hole that are low compared to the flop, with little or no chance for a straight or flush.
Side Bets
The only side bet I am aware of for this game is known as the AA+. It pays based on the poker value of the player's hand after the flop. There are three known pay tables, as follows:
AA+ Pay Tables
| Hand | Pay Table 1 | Pay Table 2 | Pay Table 3 |
|---|---|---|---|
| Royal Flush | 25 | 100 | 100 |
| Straight flush | 25 | 50 | 50 |
| 4 of a kind | 25 | 40 | 40 |
| Full house | 25 | 30 | 30 |
| Flush | 25 | 20 | 20 |
| Straight | 7 | 7 | 10 |
| Three of a kind | 7 | 7 | 8 |
| Two pair | 7 | 7 | 7 |
| Pair of aces | 7 | 7 | 7 |
| House edge | 6.40% | 6.26% | 2.97% |
Pay tables 1 and 2 can be found in land casinos. Pay table 3 is used by Internet casinos using Gamesys software.
As an example, following is the full return table for Pay Table 1.
AA+ Side Bet — Pay Table 1
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal Flush | 25 | 4 | 0.000002 | 0.000038 |
| Straight flush | 25 | 36 | 0.000014 | 0.000346 |
| 4 of a kind | 25 | 624 | 0.000240 | 0.006002 |
| Full house | 25 | 3744 | 0.001441 | 0.036014 |
| Flush | 25 | 5108 | 0.001965 | 0.049135 |
| Straight | 7 | 10200 | 0.003925 | 0.027473 |
| Three of a kind | 7 | 54912 | 0.021128 | 0.147899 |
| Two pair | 7 | 123552 | 0.047539 | 0.332773 |
| Pair of aces | 7 | 84480 | 0.032505 | 0.227537 |
| Other | -1 | 2316300 | 0.891241 | -0.891241 |
| Total | 2598960 | 1 | -0.064023 |
Progressive Jackpot
The Progressive Jackpot bet shall pay based on the player's two hole cards and the five community cards only. It does not matter whether or not the player folds or loses to the dealer. In the event of a straight flush or royal flush on the board, all players who made the Progressive Jackpot bet shall split the win.
The following table shows the probability and contribution to the return for each event. Obviously, the return from the top two awards will depend on the jackpot size, so are treated as unknowns.
Progressive Jackpot
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Royal flush | Jackpot | 4,324 | 0.000032 | x |
| Straight flush | 10% of Jackpot | 37,260 | 0.000279 | y |
| 4 of a kind | $100.00 | 224,848 | 0.001681 | 0.168100 |
| Full house | $10.00 | 3,473,184 | 0.025961 | 0.259610 |
| Other | $0.00 | 130,044,944 | 0.972047 | 0.000000 |
| Total | $0.00 | 133,784,560 | 1.000000 | 0.487931+x+y |
The table above shows the fixed wins return 42.77% of the amount bet. Assuming the player is playing alone, for every $1,000 in the meter the return will increase by 6.02%. Under the same assumption, the break-even point is $9,503.22. Due to jackpot sharing, the return will go down slightly according to the number of other players making the bet.
Jumbo Jackpot
There is another progressive jackpot called the 'Jumbo Jackpot.' The following table shows the wins, probabilities and the contribution to the return for each type of winning hand.
Jumbo Jackpot
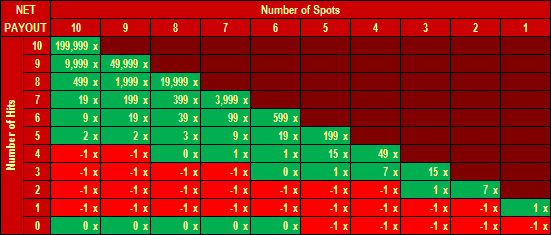
| Hand | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 7-card straight flush | ? | 32 | 0.00000024 | x |
| 6-card straight flush | $5,000.00 | 752 | 0.00000562 | 0.028105 |
| 5-card straight flush | $250.00 | 40,800 | 0.00030497 | 0.076242 |
| 4 of a kind | $50.00 | 224,848 | 0.00168067 | 0.084034 |
| Full house | $5.00 | 3,473,184 | 0.02596102 | 0.129805 |
| Flush | $4.00 | 4,047,644 | 0.03025494 | 0.121020 |
| Straight | $2.00 | 6,180,020 | 0.04619382 | 0.092388 |
| Other | $0.00 | 119,817,280 | 0.89559871 | 0.000000 |
| Total | $0.00 | 133,784,560 | 1.00000000 | 0.531593 |
The return for the top award depends on the amount in the jackpot. I can say that all the other wins return 53.16% of money bet. For every 100,000 bet units in the meter the return increases by 2.39%. At a jackpot of $1,958,300.75 the return reaches 100%.
Progressive Jackpot Side Bet
There is yet another side bet based on the player's first two cards and the three-card flop. I put information about it in my page titled Casino Hold Em Progressive Jackpot Side Bet'.
Casino Razz Bonus
I believe this side bet pays according to the poker value of the player's two hole cards and the three cards on the flop -- the lower the poker value, the more it pays. For all the rules and analysis, please see my page on Casino Razz Bonus.
Methodology
The above analysis was performed using a brute force combinatorial program that analyzed all 27,813,810,024,000 possible outcomes, and played every hand according to optimal player strategy. It took my computers about a month to crank though the 27.8 trillion hands.
External Links
The web site for Casino Hold'em, as well as other games, is www.casinopokergames.com.
There is a good Casino Hold 'Em calculator at beatingbonuses.com.
Written by:Michael Shackleford
If you spend any time at all reading about online casino games and gambling in casinos, you’ll encounter an expression—“the house edge.”
You’ll see writers explain that blackjack house edge is the lowest in the casino, and that the slots have the worst.
You’ll see them mention that some of the bets at the craps table have a house edge of less than 2%, while other bets at the craps table have a house edge of more than 16%.
But what is the house edge in a casino game and how does it work?
This site covers some similar concepts as they relate to the math of sports betting, but the casinos’ house edge works slightly differently.
Some Probability Background that Matters
You can’t understand the house edge if you don’t understand some of the basics of probability.
Probability is just a mathematical way to measure how likely something is to happen.
When a weatherman says there’s a 50% chance of rain, he’s using probability (as well as meteorology) to express that likelihood.
And most people have an intuitive understand of probability when it’s stated as a percentage, because we use it all the time.
If you paid attention in 8th grade math, you probably already know that a percentage is just another way of expressing a fraction, and that’s all a probability is—a fraction.
To determine the probability of something happening, you just look at the number of ways it could happen and divide it by the total number of possible events.
You’re rolling a 6-sided die, and you want to know what the probability of rolling a 6 is. A 6-sided die has 6 sides numbered 1 through 6. There’s only a single 6.
Since there are 6 possible outcomes, and since only one of those outcomes is a 6, the probability of rolling a 6 is 1/6.
You can convert that to a percentage of 16.67%.
You can also convert it to “odds format,” which just compares the number of ways it can’t happen with the number of ways it can. The odds of rolling a 6 on a 6-sided die are 5 to 1.
Once you have a basic understanding of probability, you can move on to the next step, which is determining the house edge of a bet.
What Is the House Edge and Why Does It Matter?
Every bet has a payout if you win and an amount you lose if you lose. This is often the same amount, or even money.
If you’re playing blackjack, you bet one unit, and most of the time, if you win, you win one unit. If you lose, you just lose that one unit.
In other words, if you bet $100 on a hand of blackjack and win, you usually win $100.
If you lose, you usually lose $100.
That’s called even money.
(And some bets in blackjack result in bigger winnings, and you sometimes have the option of surrendering, which means you only lose half your stake. But that’s a complication that doesn’t help you understand the house edge, so I’m going to save that discussion for another blog post.)
A bet’s payout can also be expressed using odds, though.
An even-money bet pays off at 1 to 1.
A bet that pays off at 5 to 1 is also possible—if you win, you get 5 units, but if you lose, you only lose 1 unit.
In the die-rolling probability example I used above, if you have a payout of 5 to 1, you’re playing a game with no house edge.
That’s because in the long run, you’ll win as much money as you lose.
But suppose I reduced the payout for rolling a 6 to 4 to 1?
You can use statistics to determine an average amount you’ll lose per bet in this situation.
You assume 6 statistically perfect rolls of the die. This means you’ll win once and lose 5 times.
If you’re betting $100 every time, you’ll have a single win of $400 along with 5 losses of $100 each, or a $500 total loss.
Your net loss after that is $100.
Since that’s a net loss of $100 over 6 bets, you’ve lost an average of $16.67 per bet.
That’s the same thing as lose 16.67% of each bet, and that percentage is the house edge.
There are other ways to arrive at that number, but that’s the easiest method I’ve seen used.
With every online casino game you play, the house pays off your bets at odds lower than the odds of winning. This results in a mathematical edge for the house.
That’s why casinos are profitable in the long run, even though every, a percentage of their customers go home with winnings in their pockets.
Probabilities—and the house edge—are always long-term phenomena. In the short run, anything can happen.
Individual online casino gamblers are always playing in the short term.
Online casinos are always playing in the long term.
If the House Has an Edge, Why Do People Still Play Casino Games?
So if, in the long run, the house can’t lose because of the math behind the games, why do people still play?
The answer is simpler than you think:
I have a friend who visits the casino at least once a week. He loses money on 4 out of 5 visits to the casino, but on one of those 5 visits every month, he comes home a winner.
He doesn’t care that he’s losing money hand over fist in the long run. He just wants to keep getting that buzz from his occasional wins.
The human brain is irrational, especially when it comes to gambling.
How the House Edge for Various Casino Games Compare
The house edge is only one factor that affects how much you’re going to lose when you’re gambling on online casino games. Other factors include how many bets you place per hour and how much you’re betting every time you place a wager.
That being said, if everything else is equal, you should play the casino games with the lowest house edge.
Keep in mind, too, that game conditions affect the house edge, too.
In some blackjack games, a natural pays off at 6 to 5 odds instead of 3 to 2 odds. The house edge on such a blackjack game is higher.
And, in fact, blackjack is a good place to start a discussion of the house edge for various casino games. It’s widely known that the house edge for blackjack is between 0.5% and 1%, but that number assumes that you’re making the optimal move in every situation. The average blackjack player is probably giving up 2% or so in mistakes.
Casino House Edge Chart Printable
Craps is a game where different bets have a different house edge. If you stick with the basic bets, pass and come, you face a house edge of 1.41%, which is relatively low. The more “exciting” wagers on the craps table come with a higher house edge.
Roulette comes in 2 main versions—single zero and double zero. The double zero version of roulette is predominant in the United States, and the roulette house edge for that game is 5.26%. By removing one of the zeroes, the online casino reduces the house edge to 2.70%.
Slot machines have a house edge that varies based on the PAR sheet for the game. (That’s the logic behind the game which determines the probability of getting various combinations of symbols and the payouts for those combinations.) You can find slot machines with a house as high as 35% or as low as 5%, but you never know what the number is.
Video poker machines look like slot machines, but they offer a better house edge—if you play the hands optimally. Depending on the pay table, the house edge for video poker can be as low as 0.5% or as high as 5% or 6%.
Conclusion
And those are the basics of the house edge as it pertains to casino games.
Casino House Edge Chart
Now that you have an understanding of the probability behind casino games and how it affects your winnings and losses, are you going to be more or less likely to play casino games?
Are you going to change the amounts you bet or the games you play?
Let me know in the comments.